进制本质与计算机位宽图解

进制定义

N进制：由N个符号组成，逢N进一的计数法则。最小为0，最大为N-1。

• 二进制：0、1（逢二进一）
• 八进制：0~7（逢八进一）
• 十进制：0~9（逢十进一）
• 十六进制：0~9、A~F（逢十六进一）

进制乘法表

• 八进制 7×7 乘法表

进制间的加减乘除

加法：加法把握住N进一的思想
八进制：25+36 先算个位 5+6=3 进位1 后算十位2+3+进位1=6 结果63

减法：够减直接减 不够减需要借位，N进制则借出来的数字就是N
十六进制：36-1E，先算6-E不够减，借一位，得(16+6)-E=8,十位3被借1位，变成2.十位算式是2-1=1，则最后结果18

乘法：运算两个数字得乘积，如果乘积小于N，直接保留。大于要除以N进制 ，取商和余数，商为高位，余数为低位，并将商和余数组合起来。

除法：查表法 数字较大时：用除数除以N进制 ，取商和余数，商为高位，余数为低位，并将商和余数组合起来（要注意借位时借位的进制）

进制间转换方式

N进制转十进制 （按权相加法）：首先个位乘以N进制的0次方 十位乘以N进制的1次方 百位乘以N进制的2次方 千位乘以N进制的3次方 依次类推最后把所有结果相加 得到最终结果（任何数的零次方都等于1）
个位 × (N进制) N的0次方 个位 3×16^0=3
十位 × (N进制) N的1次方 十位 2×16^1=32
百位 × (N进制) N的2次方 百位 1×16^2=256
123—>16进制 依此类推，把所有的结果加起来就是真正的值 3+32+256=291

N进制转换十六进制：取商留余的方式操作 要转换的数除以16后取商留余
十进制：18 18÷16=商1 余数2 取商留余 结果12

十进制转换N进制（逆向排序法）：十进制数 / N进制 得到的商为高位，余数为低位 依次排列，如果商大于、等于N继续取商留余（记得进位）
以十进制的“19”转换为二进制数为例，用19除以模（在这里模就是2）然后取它的余数。
19除以2商9余1
9除以2商4余1
4除以2商2余0
2除以2商1余0
1除以2商0余1
当商为0时结束运算，并取余后反转
所以19的二进制为10011

二进制与十六进制互相转换

二进制	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
十六进制	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

背二进制与十六进制规律

2 0010 4 0100 8 1000 16 10000
3 0011 就是4-1 7 0111 就是8-1
9 1001 就是8+1
c =4+8 d是-1 d是加1
a=2+8

计算机位宽

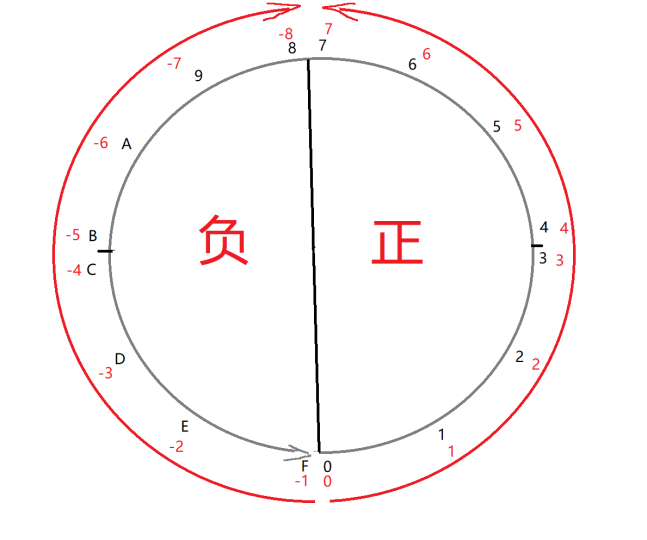
4个bit 同一个方向出发，代表正数（无符号数），最小是0x0 最大是0xF
4个bit 从0和F两个方向同时出发，在中间相遇，代表正负数（有符号数），最小是0x-8，最大是0x7

8 bit 同一个方向出发，代表正数（无符号数），最小是0x0 最大是0xFF
8 bit 从0x0和0xFF两个方向同时出发，在中间相遇，代表正负数（有符号数），最小是0x-80，最大是0x7F (8个位代表1个字节)

16 bit 同一个方向出发，代表正数（无符号数），最小是0x0 最大是0xFFFF
16 bit 从0x0和0xFFFF两个方向同时出发，在中间相遇，代表正负数（有符号数），最小是0x-8000，最大是0x7FFF (16位代表2个字节)

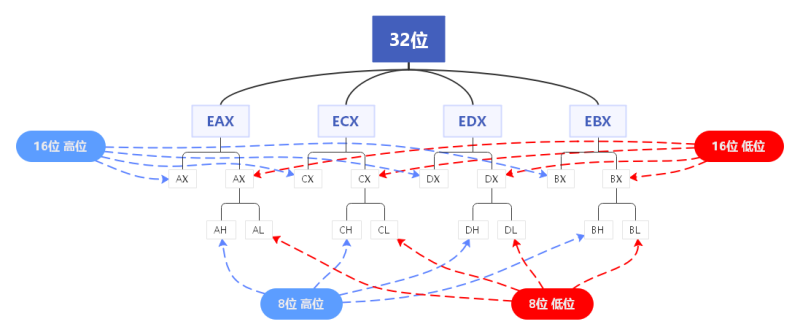
32 bit 同一个方向出发，代表正数（无符号数），最小是0x0 最大是0xFFFFFFFF
32 bit 从0x0和0xFFFFFFFF两个方向同时出发，在中间相遇，代表正负数（有符号数），最小是0x-80000000，最大是0x7FFFFFFF (32位代表4个字节)

64 bit 同一个方向出发，代表正数（无符号数），最小是0x0 最大是0xFFFFFFFFFFFFFFFF
64 bit 从0x0和0xFFFFFFFFFFFFFFFF两个方向同时出发，在中间相遇，代表正负数（有符号数），最小是0x-8000000000000000，最大是0x7FFFFFFFFFFFFFFF (64位代表8个字节)

8个bit=1个字节，4个bit=半字节
16个bit=2个字节—>字
32个bit=4个字节—>双字
8位是二进制八个位
0x 代表16进制数
两个字节=1个中文字
有符号数 有正负之分 无符号都是正数
高位1 低位0 负数1 正数0